Implementing Hopfield Networks on Coupled-Oscillator Accelerators
Thanks for the (associative) memories!
Last week, I described DIMPLE: Digital Ising Machines from Programmable Logic, Easily! It’s an FPGA implementation of an all-digital coupled-oscillator Ising machine, and it’s capable of solving certain optimization problems efficiently. (If you haven’t read that post, go back and do that!) I also alluded to one potential application for DIMPLE: accelerating machine learning (ML) algorithms. Here, I’m taking the first step towards using DIMPLE for ML by running a simple network that’s highly amenable to coupled oscillator architectures: a Hopfield network.
Hopfield networks are simple and straightforward enough for anybody to understand without a background in ML, and can serve as a good example for how architectures like DIMPLE can be used for ML applications. But a Hopfield network is just scratching the surface of what Ising machines could do for machine learning; there are many kinds of models where Ising machines could be very useful. DIMPLE is entirely open-source, and if you want to help develop more powerful and complex software to leverage it, check out our Discord, and find the main project page at unphased.ai!
What is a Hopfield network?
Like most neural networks, Hopfield networks consist of an array of neurons. Each neuron can take a value of +1 or -1, and each neuron is connected to every other neuron in the network. A Hopfield network with N neurons takes N-element vectors as inputs, and produces N-element vectors as outputs; each vectors’ elements can only be +1 and -1.
Inputs are fed to the network by setting the initial values of neurons in the network to the values of the input vector. Similarly, outputs are read from the network by reading the final values of those same neurons after the network is finished computing.

Like most machine learning models, Hopfield networks are first trained, then they are used to perform a specific task. In the case of a Hopfield network, that task is associative memory. First, the training process involves presenting the network with a number of “training vectors” (in our case, images) to remember. Then, the inference process consists of presenting the network with an input vector, and letting the network remember which training vector is most similar to the input vector.
At a high level, inference involves minimizing the total network weight of the network. By “total network weight,” I mean the sum of each weight multiplied by the values of the two neurons it connects. This quantity is usually called the network’s “energy,” and the formulation looks a lot like an Ising spin glass Hamiltonian:
These weights are determined by training the network. Most Hopfield networks are trained using one-shot Hebbian learning; essentially, you only need to present a training vector to a Hopfield network a single time to get the network to remember that vector. Plus, the calculations you need to perform to encode that training vector in the network’s weights is fairly simple. The equation for the Hebbian learning rule is shown below:
In essence, we take the vector we want to remember, and calculate the weights that would minimize the total network weight when the neurons store that vector. By averaging the weights for every training vector, we can get the network to remember many different vectors. There are some other learning rules Hopfield networks can use, but Hebbian learning is the most common, and it’s also the one we’ll be using in this work.
In my opinion, the best overview of Hopfield networks is this Towards Data Science article. For a deeper dive into Hopfield networks, this article is a great place to start.
How does DIMPLE accelerate Hopfield networks?
DIMPLE accelerates the inference (or “remembering”) process in these Hopfield networks. However, DIMPLE doesn’t accelerate Hopfield network training. Luckily, the Hebbian learning process described above is pretty simple, so accelerating training isn’t all that important. The inference process is much more difficult, because it involves solving a many-dimensional optimization problem.
Remember how the Hopfield network energy function has the same structure as an Ising Hamiltonian? Well, because DIMPLE is an Ising machine, it’s naturally well-suited for minimizing the Hopfield network energy. By solving this many-dimensional optimization problem, DIMPLE performs the Hopfield inference operation.

To map a Hopfield network to DIMPLE, we simply set each oscillator coupling weight to the corresponding connection weight in the Hopfield network. Then, we set DIMPLE’s initial spins equal to the input vector. When the DIMPLE solver settles to an optimal solution, that solution should correspond to the training vector recalled by the Hopfield network.
Measurement Results
Successful Recall
DIMPLE currently only supports 64 spins, so we tested our Hopfield networks using 8x8 monochrome images. First, we precomputed coupling weights such that the network encodes the two images shown in Figure 1: a box, and a checkerboard pattern.
Then, we set the initial Ising spin values of DIMPLE to a noisy version of one of the images. DIMPLE should automatically converge to the denoised version of the image; this is the associative memory property of the Hopfield network. And that’s exactly the behavior we observe!
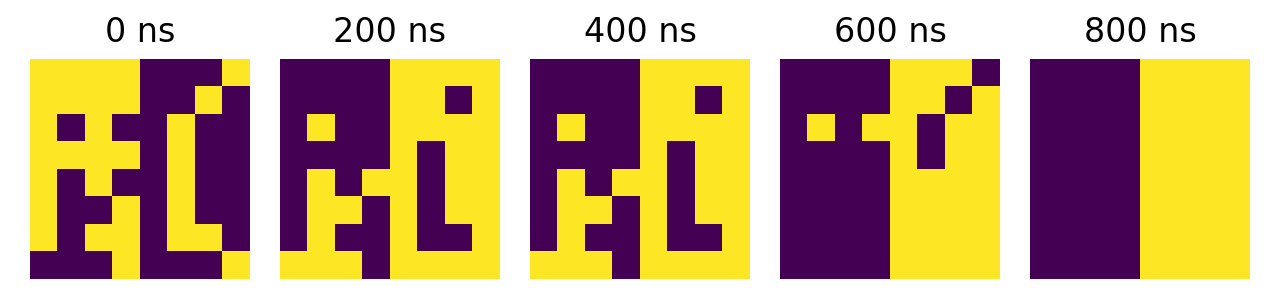
When DIMPLE is presented with an input image containing the checkerboard with added noise, shown on the left in Figure 2, it settles to Ising spin values corresponding to the image of an (almost) clean checkerboard on the right. The same behavior can be seen for an input image containing a noisy box.
Recall Speed
Next, we wanted to determine how quickly DIMPLE was able to recall images. During a recall operation, we measured the spins every 20 cycles, resulting in the images shown in Figure 3. In our example, we were able to observe successful recall within 200 clock cycles, or 800 nanoseconds with our 250MHz clock.
To build a more robust understanding of DIMPLE’s performance, we tested the recall speed for images with different amounts of noise, as shown in Figure 4. For each noise level, we let the system settle for different time periods, then measured how accurate the result was compared to the desired checkerboard image. Unsurprisingly, images with less noise were recalled more quickly, while images with more noise took longer to recall. In these tests, a noise level of 5 indicates that 5 random pixels in the initial image were inverted from their expected value.
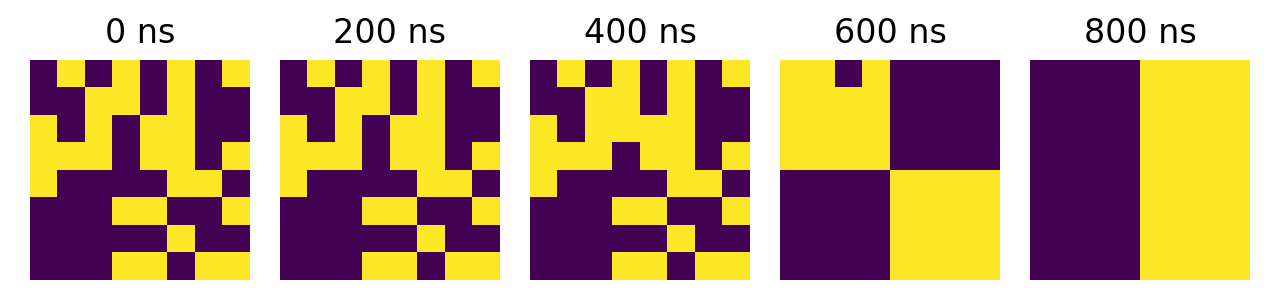
Sometimes, over time, the system’s state “jumps” from one local minimum to another. The red dotted line in Figure 4 corresponds to the accuracy score the DIMPLE would achieve if it settled to the box image; by 1200ns, some trials settled closer to the box rather than the checkerboard. A single example of this behavior is shown in Figure 5. We believe this may be due to system drift, where certain oscillators naturally run faster than others and cause the system state to shift over time. (It may also simply be due to thermal noise.) This could be mitigated by using Xilinx’s manual routing features to ensure that oscillators are all the same length.
Storage Capacity
We also wanted to understand DIMPLE’s ability to store many images before recall became disrupted. The storage capacity of Hopfield networks is already well-understood, but we expect DIMPLE to have somewhat reduced capacity due to non-idealities in the physical oscillators. DIMPLE also has limited weight resolution; our current implementation features integer weights for each coupling between -7 and +7.
A standard Hopfield network can recall 0.14N patterns, where N is the number of neurons. That means that our 64-neuron network should be able to store and recall up to 8 patterns. For our test, we selected 10 total patterns, shown in Figure 6. This means that we should be able to observe successful pattern storage at first, and then pattern storage breakdown once we try to store more than 8 patterns.
To test storage capacity, we initialized DIMPLE’s spins to each of the memorized patterns, with added noise. Then, we used DIMPLE to perform Hopfield inference, and measured the difference between the result and the same initialized image. If the pattern is properly stored, DIMPLE should remain stable at the image at which it was initialized.
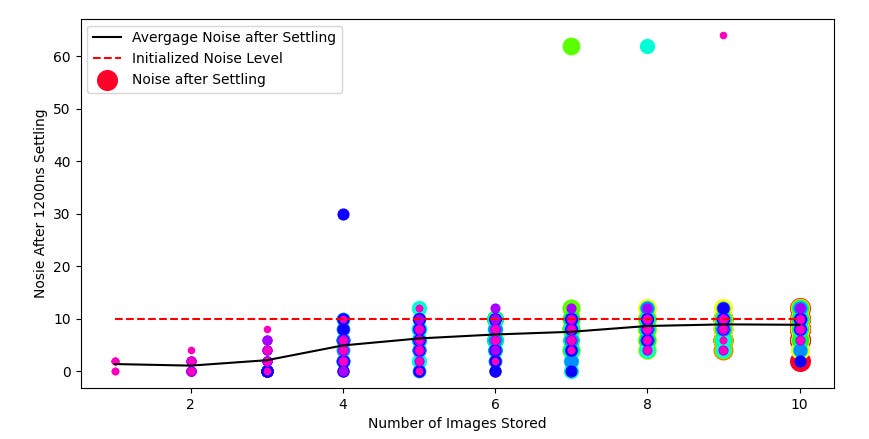
We performed these tests with 10 different sets of DIMPLE weights to obtain Figure 7. For each set of weights, we stored another image. This helped us understand at which point DIMPLE stopped being able to properly recall images.
Surprisingly, DIMPLE was able to effectively store all 8 images. Occasionally, DIMPLE would fail to settle, and the measured noise would be fairly high, but in most cases, DIMPLE’s result was closer to the target image than the initialization value was. However, we can clearly see that, as more images are stored, the recall process slows and becomes less exact, and input images are less likely to settle exactly to the closest stored image.
Future Work
We think there are ways to improve DIMPLE’s performance on Hopfield networks. As discussed above, DIMPLE sometimes “jumps” from one local minimum to another. By optimizing the physical layout of the DIMPLE core matrix and leveraging manual routing we can potentially increase the stability of each local minimum and make DIMPLE more practical for Hopfield network inference.
Also, all of this work has focused on the basic, mid-1980’s version of Hopfield networks. There’s been a lot of modern research on more powerful variants of Hopfield networks, with networks that support continuous weight values, methods for increasing storage capacity, and sparse networks that offer better performance than their dense counterparts. There’s potential for DIMPLE to accelerate some of these more modern Hopfield networks, too, which may require updates to the DIMPLE hardware and software stack.
We’re going to keep working to find new, exciting applications for DIMPLE! If you want to help, check out our Discord, and find the main project page at unphased.ai.