Approximate Computing for Secure AI Chips
A new use-case for approximate computing.
Side-channel security has been a major concern for secure hardware for a long time. Since the late 1990s, researchers have been trying to develop implementations of cryptographic algorithms that avoid leaking secret information through their patterns of power consumption or electromagnetic radiation. This process is difficult, but well-scoped: given a specific algorithm, like AES-256, researchers need to develop a side-channel secure hardware implementation with the best overall performance.
Recently, though, researchers and industry experts have started to consider what side-channel secure AI chips would be like. AI chips are very different from cryptography ASICs; instead of building a single-purpose secure block that runs a single algorithm, chip designers need to build a re-programmable core capable of accelerating many AI algorithms. Given the size and complexity of modern AI chips, it seems prohibitively costly to leverage state-of-the-art security techniques like masking or threshold implementations to secure their logic.
So if companies like OpenAI want secure AI chips, how can we make them? According to a group from MIT, the answer might lie in approximate arithmetic. Today, we’re going to be diving into their paper, which demonstrates the most efficient side-channel secure AI chip ever proposed.
What is approximate arithmetic?
If you’re building a cryptographic algorithm, all of your mathematical operations need to be exact. If you flip one bit in your AES block cipher, the result is totally incoherent. But AI algorithms are relatively robust to errors, especially during inference. We regularly quantize AI models to 16-bit, 8-bit, and even 4-bit weights; this quantization can be thought of as a very simple form of approximate arithmetic. Instead of doing expensive, full-precision 32-bit calculations, we make do with 4-bit calculations.
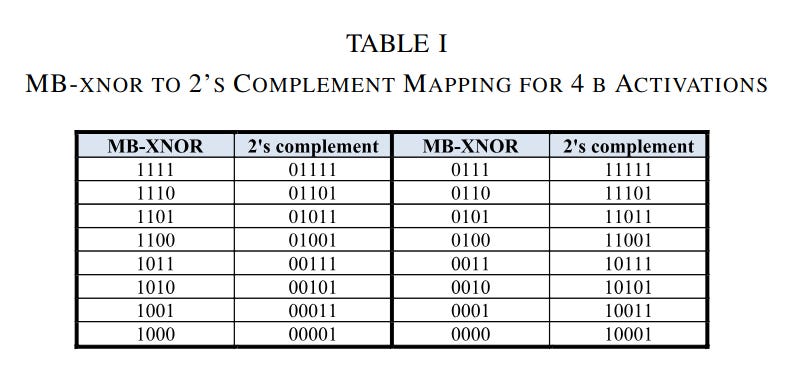
But there are different kinds of approximations you can make, too. Some kinds of approximate computing leverage number formats that make arithmetic logic much simpler. In their quest to build ultra-efficient AI chips, a group of Columbia University researchers proposed a number format they called MB-XNOR. In MB-XNOR, bit N in a number represents a value of 2N if the bit is 1, and represents a value of -2N if the bit is 0. MB-XNOR numbers map to 2’s complement numbers according to the following table.
The observant among you can probably identify that MB-XNOR doesn’t feature a way to represent the number zero. This is what makes it approximate -- it can’t represent all the numbers you might want to represent. But it also makes certain kinds of math much easier to implement. If you use 1-bit network activations, with a 1 representing +1 and a 0 representing -1, you can do 4-bit-by-1-bit multiplication entirely using XNOR gates. This lends itself to very compact and efficient multipliers, which are particularly useful for in-memory computing schemes, as shown in Figure 4 from their paper.
It turns out, though, that approximate number formats like MB-XNOR may offer more than just performance and efficiency benefits. These number formats may offer a unique way to boost the security of AI chips.
How can approximate arithmetic make AI chips more secure?
As we’ve discussed previously on the blog, the power consumption of circuits can depend on the data that those circuits are processing. So, if you measure the power consumption of a circuit processing secret data, you can eventually extract the secret data. This technique, called differential power analysis, can be used to steal weights from AI chips. And because models can cost millions of dollars to train, stealing AI model weights is a big deal.
Luckily, there are techniques that can secure chips, so that power consumption and secret data become uncorrelated. If you generate a series of random bits called a mask, and XOR that mask with your data, you can send the masked data along wires without causing side-channel leakage.
This simple masking technique works when you’re sending data along a wire. It also works for some logic gates. For example, assume we’re masking two input bits, X and Y, using masks M1 and M2, respectively. If you perform an XOR operation on the masked values and also on the masks, you can then reconstruct the original XOR of X and Y easily using another XOR operation. More formally:
But this masking technique doesn’t work for all kinds of logic gates. If you wanted to do the same thing with an AND gate, you wouldn’t be able to reconstruct the desired AND result so simply.
Gates like AND and OR, which are called nonlinear gates, are hard to mask. It’s certainly not impossible, but masked circuits for nonlinear gates often are fairly large, expensive, and have security flaws. HPC4, a state-of-the-art masked AND gate, requires multiple registers, multiplexers, and complex multi-input gates to implement a single AND gate. It also requires additional random bits to be added to every gate on every cycle to “refresh” the random state of the mask.
Often, side-channel secure implementations of complex circuits can be over five times larger and much slower than their insecure counterparts, while also requiring thousands of random bits to be generated every cycle to refresh their gates. This may not be a huge issue for simple circuits like AES block ciphers, but making an AI chip five times larger and slower would be a major issue. This is exacerbated by the kinds of operations that AI chips actually implement: vector-matrix multiplication. Multiplication uses a lot of AND gates; a 2-bit multiplier uses 6 AND gates, and it only gets worse from there.
This is where MB-XNOR becomes incredibly useful. It’s very easy to mask XNOR gates, as they’re linear gates. If we use a multiplication scheme that replaces most of our AND gates with OR gates, we can build a side-channel-secure multiplier with far fewer gates. And that’s precisely what this paper from MIT focuses on. By leveraging MB-XNOR based approximate multiplication, they reduce their circuit area by a factor of 8, while also requiring zero random bits for mask refreshing.
This sort of co-design, where we select special circuit architectures that are easy to secure, isn’t possible for conventional cryptographic accelerators. For cryptographic chips, the algorithm is set in stone, and can’t be modified without becoming noncompliant with the standard implementation. AI chips represent the first time when it makes sense to change the mathematical operations being done by a chip to make it easier to secure.
And approximate arithmetic using MB-XNOR logic is just the starting point. It’s still a fairly un-optimized design; multi-bit activations have to be handled bit-serially, and have limited bit precision. And though this specific paper doesn’t report on neural network accuracy, MB-XNOR has been shown to decrease accuracy on CIFAR10 by 1-2%, while other efficient and secure AI chips have been reported to decrease accuracy by up to 5%.
Approximate computing could be the best way to secure AI computation in a practical, efficient, and cost-effective manner. But there’s still a long ways to go before it becomes practical enough for a commercial AI chip.